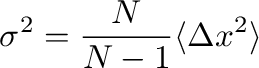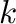 -th moment
-th moment
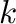 -th moment
-th moment
![\includegraphics[height=10mm]{images/moment}% WIDTH=48 HEIGHT=45](img189.png)
The operator can be placed on the canvas in two ways:
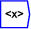 ;
or
;
or
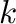 -th moment about the mean along a named dimension
of all elements present.
-th moment about the mean along a named dimension
of all elements present. 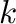 is specified by the numerical argument
of the operation, which defaults to 1 (hence the result will be 0
in that case). If the dimension is not named, then the
is specified by the numerical argument
of the operation, which defaults to 1 (hence the result will be 0
in that case). If the dimension is not named, then the 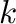 -th moment
is over all elements present in the tensor. Note that missing elements
are not counted.
-th moment
is over all elements present in the tensor. Note that missing elements
are not counted.
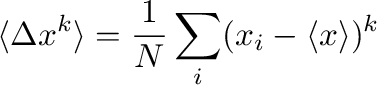
Also