Functions | |
| vector< pair< float, float > > | allHandleCoords (vector< float > coords) |
| vector< pair< float, float > > | toCoordPair (vector< float > coords) |
| vector< vector< float > > | constructTriDiag (int length) |
| vector< pair< float, float > > | constructTargetVector (int n, const vector< pair< float, float >> &knots) |
| vector< pair< float, float > > | computeControlPoints (vector< vector< float >> triDiag, const vector< pair< float, float >> &knots, vector< pair< float, float >> target) |
| bool | segNear (float x0, float y0, float x1, float y1, float x, float y) |
| float | d2 (float x0, float y0, float x1, float y1) |
Function Documentation
◆ allHandleCoords()
| vector<pair<float,float> > minsky::anonymous_namespace{wire.cc}::allHandleCoords | ( | vector< float > | coords | ) |
Definition at line 150 of file wire.cc.
Referenced by minsky::Wire::near().

◆ computeControlPoints()
| vector<pair<float,float> > minsky::anonymous_namespace{wire.cc}::computeControlPoints | ( | vector< vector< float >> | triDiag, |
| const vector< pair< float, float >> & | knots, | ||
| vector< pair< float, float >> | target | ||
| ) |
Thomas' algorithm for solving a matrix equation \(Ac=k\) is based on LU-decomposition into \(LUc=k\) where \(L\) is lower triangular and \(U\) is upper triangular. The matrix equation is solved by setting \(Uc = k'\) and then solving \(Lk' = k\) for \(k'\) first, and subsequently \(Uc\) for \(c\).
There are two steps in this calculation. Step 1 involves simultaneously decomposing \(A = LU\) and solving \(Lk'=k\) for \(k'\) in a forward sweep, with \(Uc=k'\) as result. In step 2, \(Uc=k'\) is solved for \(c\) in a backward sweep. The calculation goes as follows for a small system:
\[ \left(\begin{array}{ccc} b_1 & a_1 & 0 \\ d_1 & b_2 & a_2 \\ 0 & d_2 & b_3 \end{array}\right) \left(\begin{array}{c} c_1 \\ c_2 \\ c_3 \end{array}\right) = \left(\begin{array}{c} k_1 \\ k_2 \\ k_3 \end{array}\right) \]
Forward sweep: row 1:
\( b_1c_1+a_1c_2 = k_1 \)
\( c_1+\frac{c_1}{b_1}c_2 = \frac{k_1}{b_1} \) after dividing through by \(b_1\)
Rewrite row 1 as \( c_1 + \alpha_1c_2 = k'_1\), where \(\alpha_1=\frac{c_1}{b_1}\) and \(k'_1 = \frac{k_1}{b_1}\)
row 2:
\( d_1c_1+b_2c_2+a_2c_3 = k_2 \)
Now eliminate the first term of this equation by subtracting \(d_1 \times\) row 1 from row 2, yielding:
\( (b_2 - d_1\alpha_1)c_2 + a_2c_3 = k_2 - d_1k'_1 \)
Then, dividing through by \((b_2 - d_1\alpha_1)\) and rewriting leads to:
\( c_2 + \alpha_2c_3 = k'_2 \), where \(\alpha_2 = \frac{a_2}{b_2 - d_1\alpha_1}\) and \(k'_2 = \frac{k_2 - d_1k'_1}{b_2 - d_1\alpha_1}\)
row 3:
Finally, subtracting \(d_2 \times\) row 2 from row 3, dividing through by \((b_3-d_2\alpha_2)\), and rewriting, yields:
\( c_3 = k'_3 \), where \(k'_3 = \frac{k_3-d_2k'2}{b_3 - d_2\alpha_2}\)
At this point, the matrix equation has been reduced to
\[ \left(\begin{array}{ccc} 1 & \alpha_1 & 0 \\ 0 & 1 & \alpha_2 \\ 0 & 0 & 1 \end{array}\right) \left(\begin{array}{c} c_1 \\ c_2 \\ c_3 \end{array}\right) = \left(\begin{array}{c} k'_1 \\ k'_2 \\ k'_3 \end{array}\right) \]
In this form, one can solve for the \(c_i\) in terms of \(k'_i\) directly by sweeping backwards through the matrix equation.
(Source: http://www.industrial-maths.com/ms6021_thomas.pdf)
Definition at line 283 of file wire.cc.
Referenced by minsky::Wire::draw().
◆ constructTargetVector()
| vector<pair<float,float> > minsky::anonymous_namespace{wire.cc}::constructTargetVector | ( | int | n, |
| const vector< pair< float, float >> & | knots | ||
| ) |
Definition at line 208 of file wire.cc.
Referenced by minsky::Wire::draw().
◆ constructTriDiag()
| vector<vector<float> > minsky::anonymous_namespace{wire.cc}::constructTriDiag | ( | int | length | ) |
Definition at line 181 of file wire.cc.
Referenced by minsky::Wire::draw().
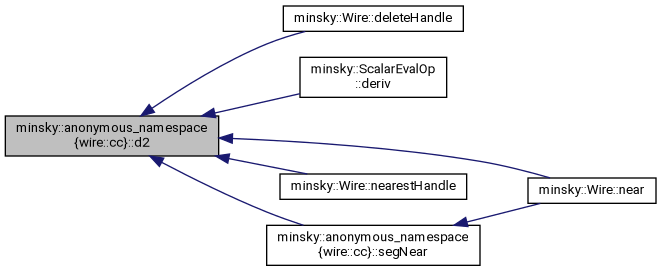
◆ d2()
|
inline |
Definition at line 564 of file wire.cc.
References minsky::sqr().
Referenced by minsky::Wire::deleteHandle(), minsky::ScalarEvalOp::deriv(), minsky::Wire::near(), minsky::Wire::nearestHandle(), and segNear().

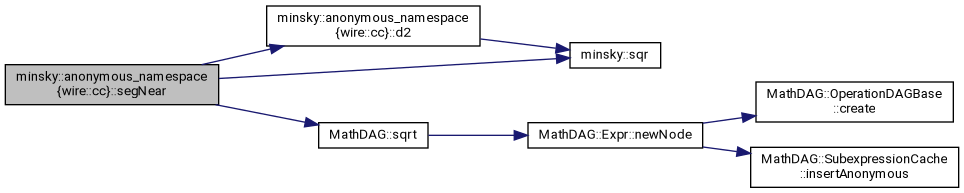
◆ segNear()
| bool minsky::anonymous_namespace{wire.cc}::segNear | ( | float | x0, |
| float | y0, | ||
| float | x1, | ||
| float | y1, | ||
| float | x, | ||
| float | y | ||
| ) |
Definition at line 557 of file wire.cc.
References d2(), minsky::sqr(), and MathDAG::sqrt().
Referenced by minsky::Wire::near().

◆ toCoordPair()
| vector<pair<float,float> > minsky::anonymous_namespace{wire.cc}::toCoordPair | ( | vector< float > | coords | ) |
Definition at line 169 of file wire.cc.
Referenced by minsky::Wire::draw().