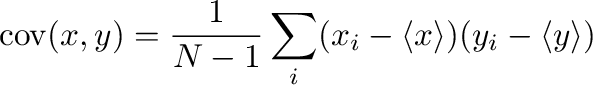Covariance

The operator can be placed on the canvas in two ways:

• From the Statistics (``statistics'') toolbar ; or
• By typing the letters ``covariance'' on the canvas and then pressing the Enter key

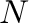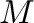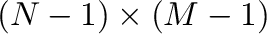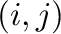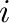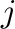Computes the covariance of two tensors along named dimension. If the inputs are of rank and respectively, the output will be a rank tensor, where the element is the covariance of the -th slice of the first argument along the named dimension, and the -th slice along the named dimension. As such, it is conformant with the definition of cov function in Octave, but not with the equivalently named function in Matlab: quoteCompatibility Note:: Octave always treats rows of X and Y as multivariate random variables. For two inputs, however, MATLAB treats X and Y as two univariate distributions regardless of their shapes, and will calculate covariance whenever the number of elements in X and Y are equal. This will result in a 2x2 matrix. Code relying on MATLAB's definition will need to be changed when running in Octave. If only a single argument 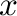is supplied to the covariance, then the result is equivalent to cov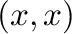, ie each slice is covaried with each other slice.

The formula for covariance between stochastic variables 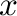and is $$\mathrm{cov}(x,y)=\frac{1}{N-1}\sum_{i}(x_{i}-\langle x\rangle)(y_{i}-\langle y\rangle) \end{displaymath}% WIDTH=593 HEIGHT=85$$