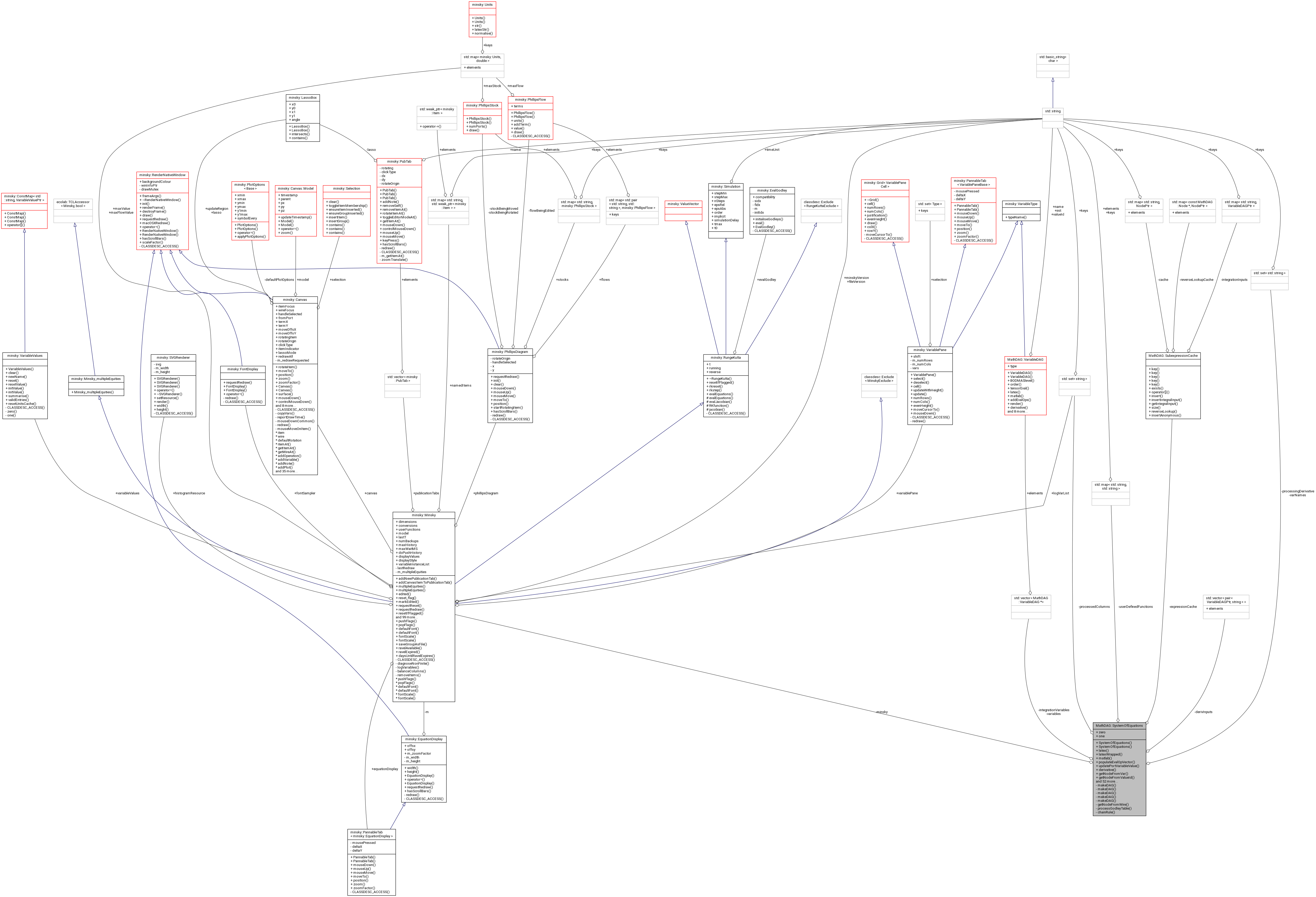
#include <equations.h>
Public Attributes | |
| NodePtr | zero {new ConstantDAG("0")} |
| useful constants to share More... | |
| NodePtr | one {new ConstantDAG("1")} |
Private Member Functions | |
| NodePtr | makeDAG (const string &valueId, const string &name, VariableType::Type type) |
| create a variable DAG. returns cached value if previously called More... | |
| NodePtr | makeDAG (VariableBase &v) |
| NodePtr | makeDAG (const OperationBase &op) |
| create an operation DAG. returns cached value if previously called More... | |
| NodePtr | makeDAG (const SwitchIcon &op) |
| NodePtr | makeDAG (const Lock &op) |
| NodePtr | getNodeFromWire (const Wire &wire) |
| returns cached subexpression node representing what feeds the wire, creating a new one if necessary More... | |
| void | processGodleyTable (map< string, GodleyColumnDAG > &godleyVariables, const GodleyIcon &) |
| template<class Expr > | |
| NodePtr | chainRule (const Expr &x, const Expr &deriv) |
| applies the chain rule to expression x More... | |
Private Attributes | |
| SubexpressionCache | expressionCache |
| vector< VariableDAG * > | variables |
| vector< VariableDAG * > | integrationVariables |
| set< string > | processedColumns |
| vector< pair< VariableDAGPtr, string > > | derivInputs |
| const Minsky & | minsky |
| std::set< std::string > | varNames |
| used to rename ambiguous variables in different scopes More... | |
| std::set< std::string > | processingDerivative |
| keep track of derivatives of variables, to trap definition loops More... | |
| std::map< std::string, std::string > | userDefinedFunctions |
| table of user defined functions and their definitions More... | |
Detailed Description
Definition at line 358 of file equations.h.
Constructor & Destructor Documentation
◆ SystemOfEquations() [1/2]
construct the system of equations
Definition at line 460 of file equations.cc.
References minsky::Minsky::canvas, derivInputs, expressionCache, MathDAG::SubexpressionCache::getIntegralInput(), getNodeFromWire(), minsky::group, minsky::GroupItems::groups, MathDAG::SubexpressionCache::insertAnonymous(), MathDAG::SubexpressionCache::insertIntegralInput(), integrationVariables, MathDAG::VariableDAG::intOp, minsky::Canvas::itemIndicator, minsky::GroupItems::items, makeDAG(), minsky::minsky(), minsky::Minsky::model, MathDAG::VariableDAG::name, one, processGodleyTable(), MathDAG::VariableDAG::rhs, MathDAG::SubexpressionCache::size(), minsky::VariableType::stock, minsky::VariableType::typeName(), minsky::uqName(), userDefinedFunctions, variables, minsky::Minsky::variableValues, and zero.
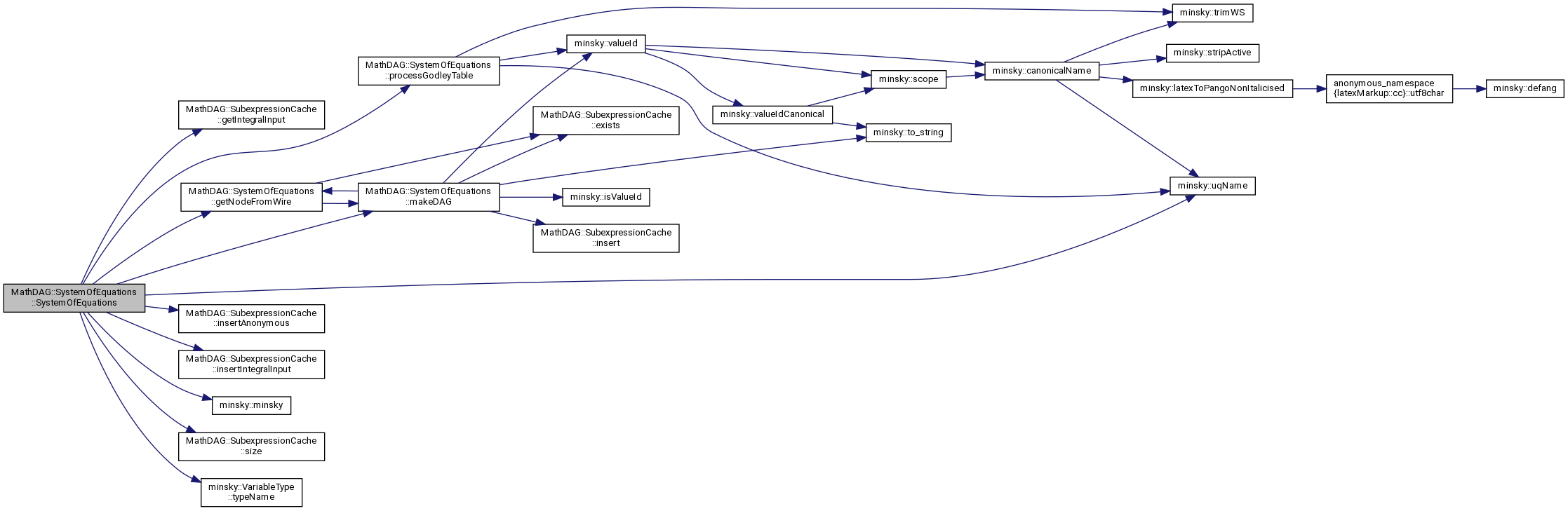
◆ SystemOfEquations() [2/2]
| MathDAG::SystemOfEquations::SystemOfEquations | ( | const Minsky & | m | ) |
Definition at line 457 of file equations.cc.
Member Function Documentation
◆ chainRule() [1/2]
Definition at line 68 of file derivative.cc.
◆ chainRule() [2/2]
|
private |
applies the chain rule to expression x
◆ derivative() [1/49]
| NodePtr MathDAG::SystemOfEquations::derivative | ( | const VariableDAG & | expr | ) |
Definition at line 80 of file derivative.cc.
References MathDAG::Node::derivative(), MathDAG::differentiateName(), minsky::VariableType::integral, MathDAG::VariableDAG::name, MathDAG::VariableDAG::rhs, minsky::VariableType::stock, minsky::VariableType::tempFlow, MathDAG::VariableDAG::type, and MathDAG::VariableDAG::valueId.

◆ derivative() [2/49]
| NodePtr MathDAG::SystemOfEquations::derivative | ( | const ConstantDAG & | ) |
Definition at line 114 of file derivative.cc.
◆ derivative() [3/49]
| NodePtr MathDAG::SystemOfEquations::derivative | ( | const OperationDAG< OperationType::constant > & | expr | ) |
Definition at line 121 of file derivative.cc.
◆ derivative() [4/49]
| NodePtr MathDAG::SystemOfEquations::derivative | ( | const OperationDAG< OperationType::add > & | expr | ) |
Definition at line 128 of file derivative.cc.
References MathDAG::OperationDAGBase::arguments.
◆ derivative() [5/49]
| NodePtr MathDAG::SystemOfEquations::derivative | ( | const OperationDAG< OperationType::subtract > & | expr | ) |
Definition at line 145 of file derivative.cc.
References MathDAG::OperationDAGBase::arguments.
◆ derivative() [6/49]
| NodePtr MathDAG::SystemOfEquations::derivative | ( | const OperationDAG< OperationType::multiply > & | expr | ) |
Definition at line 158 of file derivative.cc.
References MathDAG::OperationDAGBase::arguments.
◆ derivative() [7/49]
| NodePtr MathDAG::SystemOfEquations::derivative | ( | const OperationDAG< OperationType::divide > & | expr | ) |
Definition at line 190 of file derivative.cc.
References MathDAG::OperationDAGBase::arguments.
◆ derivative() [8/49]
| NodePtr MathDAG::SystemOfEquations::derivative | ( | const OperationDAG< OperationType::log > & | expr | ) |
Definition at line 221 of file derivative.cc.
References MathDAG::OperationDAGBase::arguments, and MathDAG::log().

◆ derivative() [9/49]
| NodePtr MathDAG::SystemOfEquations::derivative | ( | const OperationDAG< OperationType::pow > & | expr | ) |
Definition at line 237 of file derivative.cc.
References MathDAG::OperationDAGBase::arguments, MathDAG::exp(), and MathDAG::log().

◆ derivative() [10/49]
| NodePtr MathDAG::SystemOfEquations::derivative | ( | const OperationDAG< OperationType::lt > & | expr | ) |
◆ derivative() [11/49]
| NodePtr MathDAG::SystemOfEquations::derivative | ( | const OperationDAG< OperationType::le > & | expr | ) |
◆ derivative() [12/49]
| NodePtr MathDAG::SystemOfEquations::derivative | ( | const OperationDAG< OperationType::eq > & | expr | ) |
◆ derivative() [13/49]
| NodePtr MathDAG::SystemOfEquations::derivative | ( | const OperationDAG< OperationType::and_ > & | expr | ) |
Definition at line 283 of file derivative.cc.
◆ derivative() [14/49]
| NodePtr MathDAG::SystemOfEquations::derivative | ( | const OperationDAG< OperationType::or_ > & | expr | ) |
Definition at line 290 of file derivative.cc.
◆ derivative() [15/49]
| NodePtr MathDAG::SystemOfEquations::derivative | ( | const OperationDAG< OperationType::not_ > & | expr | ) |
Definition at line 297 of file derivative.cc.
◆ derivative() [16/49]
| NodePtr MathDAG::SystemOfEquations::derivative | ( | const OperationDAG< OperationType::min > & | expr | ) |
Definition at line 306 of file derivative.cc.
References MathDAG::OperationDAGBase::arguments.
◆ derivative() [17/49]
| NodePtr MathDAG::SystemOfEquations::derivative | ( | const OperationDAG< OperationType::max > & | expr | ) |
Definition at line 336 of file derivative.cc.
References MathDAG::OperationDAGBase::arguments.
◆ derivative() [18/49]
| NodePtr MathDAG::SystemOfEquations::derivative | ( | const OperationDAG< OperationType::time > & | expr | ) |
Definition at line 364 of file derivative.cc.
◆ derivative() [19/49]
| NodePtr MathDAG::SystemOfEquations::derivative | ( | const OperationDAG< OperationType::euler > & | expr | ) |
Definition at line 371 of file derivative.cc.
◆ derivative() [20/49]
| NodePtr MathDAG::SystemOfEquations::derivative | ( | const OperationDAG< OperationType::pi > & | expr | ) |
Definition at line 378 of file derivative.cc.
◆ derivative() [21/49]
| NodePtr MathDAG::SystemOfEquations::derivative | ( | const OperationDAG< OperationType::zero > & | expr | ) |
Definition at line 385 of file derivative.cc.
◆ derivative() [22/49]
| NodePtr MathDAG::SystemOfEquations::derivative | ( | const OperationDAG< OperationType::one > & | expr | ) |
Definition at line 392 of file derivative.cc.
◆ derivative() [23/49]
| NodePtr MathDAG::SystemOfEquations::derivative | ( | const OperationDAG< OperationType::inf > & | expr | ) |
Definition at line 399 of file derivative.cc.
◆ derivative() [24/49]
| NodePtr MathDAG::SystemOfEquations::derivative | ( | const OperationDAG< OperationType::percent > & | expr | ) |
Definition at line 406 of file derivative.cc.
References MathDAG::OperationDAGBase::arguments.
◆ derivative() [25/49]
| NodePtr MathDAG::SystemOfEquations::derivative | ( | const OperationDAG< OperationType::copy > & | expr | ) |
◆ derivative() [26/49]
symbolically differentiate expr
◆ derivative() [27/49]
| NodePtr MathDAG::SystemOfEquations::derivative | ( | const OperationDAG< OperationType::integrate > & | expr | ) |
Definition at line 425 of file derivative.cc.
◆ derivative() [28/49]
| NodePtr MathDAG::SystemOfEquations::derivative | ( | const OperationDAG< OperationType::differentiate > & | expr | ) |
Definition at line 432 of file derivative.cc.
◆ derivative() [29/49]
| NodePtr MathDAG::SystemOfEquations::derivative | ( | const OperationDAG< OperationType::data > & | expr | ) |
Definition at line 439 of file derivative.cc.
◆ derivative() [30/49]
| NodePtr MathDAG::SystemOfEquations::derivative | ( | const OperationDAG< OperationType::ravel > & | expr | ) |
Definition at line 446 of file derivative.cc.
◆ derivative() [31/49]
| NodePtr MathDAG::SystemOfEquations::derivative | ( | const OperationDAG< OperationType::sqrt > & | expr | ) |
Definition at line 453 of file derivative.cc.
References MathDAG::OperationDAGBase::arguments, and MathDAG::sqrt().

◆ derivative() [32/49]
| NodePtr MathDAG::SystemOfEquations::derivative | ( | const OperationDAG< OperationType::exp > & | expr | ) |
Definition at line 463 of file derivative.cc.
References MathDAG::OperationDAGBase::arguments, and MathDAG::exp().

◆ derivative() [33/49]
| NodePtr MathDAG::SystemOfEquations::derivative | ( | const OperationDAG< OperationType::ln > & | expr | ) |
Definition at line 474 of file derivative.cc.
References MathDAG::OperationDAGBase::arguments.
◆ derivative() [34/49]
| NodePtr MathDAG::SystemOfEquations::derivative | ( | const OperationDAG< OperationType::sin > & | expr | ) |
Definition at line 484 of file derivative.cc.
References MathDAG::OperationDAGBase::arguments, and MathDAG::cos().

◆ derivative() [35/49]
| NodePtr MathDAG::SystemOfEquations::derivative | ( | const OperationDAG< OperationType::cos > & | expr | ) |
Definition at line 494 of file derivative.cc.
References MathDAG::OperationDAGBase::arguments, and MathDAG::sin().

◆ derivative() [36/49]
| NodePtr MathDAG::SystemOfEquations::derivative | ( | const OperationDAG< OperationType::tan > & | expr | ) |
Definition at line 505 of file derivative.cc.
References MathDAG::OperationDAGBase::arguments, and MathDAG::cos().

◆ derivative() [37/49]
| NodePtr MathDAG::SystemOfEquations::derivative | ( | const OperationDAG< OperationType::asin > & | expr | ) |
Definition at line 516 of file derivative.cc.
References MathDAG::OperationDAGBase::arguments, and MathDAG::sqrt().

◆ derivative() [38/49]
| NodePtr MathDAG::SystemOfEquations::derivative | ( | const OperationDAG< OperationType::acos > & | expr | ) |
Definition at line 526 of file derivative.cc.
References MathDAG::OperationDAGBase::arguments, and MathDAG::sqrt().

◆ derivative() [39/49]
| NodePtr MathDAG::SystemOfEquations::derivative | ( | const OperationDAG< OperationType::atan > & | expr | ) |
Definition at line 536 of file derivative.cc.
References MathDAG::OperationDAGBase::arguments.
◆ derivative() [40/49]
| NodePtr MathDAG::SystemOfEquations::derivative | ( | const OperationDAG< OperationType::sinh > & | expr | ) |
Definition at line 546 of file derivative.cc.
References MathDAG::OperationDAGBase::arguments, and MathDAG::cosh().

◆ derivative() [41/49]
| NodePtr MathDAG::SystemOfEquations::derivative | ( | const OperationDAG< OperationType::cosh > & | expr | ) |
Definition at line 556 of file derivative.cc.
References MathDAG::OperationDAGBase::arguments, and MathDAG::sinh().

◆ derivative() [42/49]
| NodePtr MathDAG::SystemOfEquations::derivative | ( | const OperationDAG< OperationType::tanh > & | expr | ) |
Definition at line 566 of file derivative.cc.
References MathDAG::OperationDAGBase::arguments, and MathDAG::cosh().

◆ derivative() [43/49]
| NodePtr MathDAG::SystemOfEquations::derivative | ( | const OperationDAG< OperationType::abs > & | expr | ) |
Definition at line 577 of file derivative.cc.
References MathDAG::OperationDAGBase::arguments.
◆ derivative() [44/49]
| NodePtr MathDAG::SystemOfEquations::derivative | ( | const OperationDAG< OperationType::floor > & | expr | ) |
◆ derivative() [45/49]
| NodePtr MathDAG::SystemOfEquations::derivative | ( | const OperationDAG< OperationType::frac > & | expr | ) |
◆ derivative() [46/49]
| NodePtr MathDAG::SystemOfEquations::derivative | ( | const OperationDAG< OperationType::Gamma > & | expr | ) |
Definition at line 606 of file derivative.cc.
References MathDAG::OperationDAGBase::arguments, MathDAG::Gamma(), and MathDAG::polygamma().

◆ derivative() [47/49]
| NodePtr MathDAG::SystemOfEquations::derivative | ( | const OperationDAG< OperationType::polygamma > & | expr | ) |
Definition at line 616 of file derivative.cc.
References MathDAG::OperationDAGBase::arguments, and MathDAG::polygamma().

◆ derivative() [48/49]
| NodePtr MathDAG::SystemOfEquations::derivative | ( | const OperationDAG< OperationType::fact > & | expr | ) |
Definition at line 629 of file derivative.cc.
References MathDAG::OperationDAGBase::arguments, MathDAG::Gamma(), and MathDAG::polygamma().

◆ derivative() [49/49]
| NodePtr MathDAG::SystemOfEquations::derivative | ( | const OperationDAG< OperationType::userFunction > & | expr | ) |
Definition at line 639 of file derivative.cc.
◆ getDefFromIntVar()
| ostringstream MathDAG::SystemOfEquations::getDefFromIntVar | ( | const VariableBase & | v | ) |
Definition at line 891 of file equations.cc.
References expressionCache, MathDAG::SubexpressionCache::getIntegralInput(), and minsky::VariableBase::valueId().
Referenced by minsky::VariableBase::definition().


◆ getNodeFromIntVar()
|
inline |
Definition at line 423 of file equations.h.
References MathDAG::SubexpressionCache::getIntegralInput(), and minsky::valueId().
Referenced by minsky::VariableValue::summary().


◆ getNodeFromValueId()
|
inline |
Definition at line 421 of file equations.h.
Referenced by minsky::VariableValue::summary().

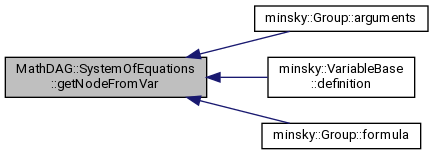
◆ getNodeFromVar()
| VariableDAGPtr MathDAG::SystemOfEquations::getNodeFromVar | ( | const VariableBase & | v | ) |
Definition at line 882 of file equations.cc.
References MathDAG::SubexpressionCache::exists(), expressionCache, makeDAG(), and minsky::VariableType::undefined.
Referenced by minsky::Group::arguments(), minsky::VariableBase::definition(), and minsky::Group::formula().

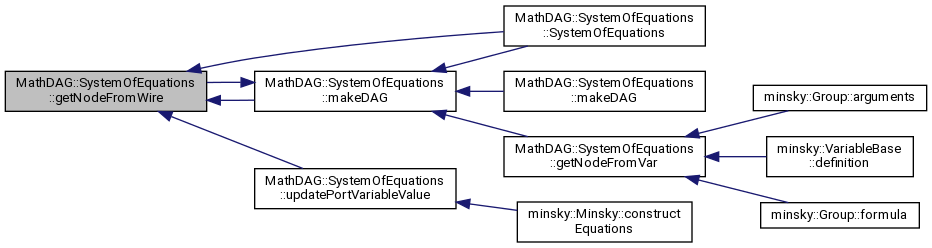
◆ getNodeFromWire()
returns cached subexpression node representing what feeds the wire, creating a new one if necessary
Definition at line 846 of file equations.cc.
References MathDAG::SubexpressionCache::exists(), expressionCache, makeDAG(), minsky::VariableType::undefined, and minsky::wire.
Referenced by makeDAG(), SystemOfEquations(), and updatePortVariableValue().

◆ latex()
| ostream & MathDAG::SystemOfEquations::latex | ( | ostream & | o | ) | const |
render as a LaTeX eqnarray Use LaTeX brqn environment to wrap long lines
Definition at line 902 of file equations.cc.
References minsky::VariableType::constant, expressionCache, MathDAG::SubexpressionCache::getIntegralInput(), integrationVariables, MathDAG::latexInit(), MathDAG::mathrm(), minsky::VariableType::tempFlow, userDefinedFunctions, and variables.
Referenced by minsky::Minsky::latex().


◆ latexWrapped()
| ostream & MathDAG::SystemOfEquations::latexWrapped | ( | ostream & | o | ) | const |
Definition at line 933 of file equations.cc.
References minsky::VariableType::constant, expressionCache, MathDAG::SubexpressionCache::getIntegralInput(), integrationVariables, MathDAG::latexInit(), MathDAG::mathrm(), minsky::VariableType::tempFlow, and variables.
Referenced by minsky::Minsky::latex().


◆ makeDAG() [1/5]
|
private |
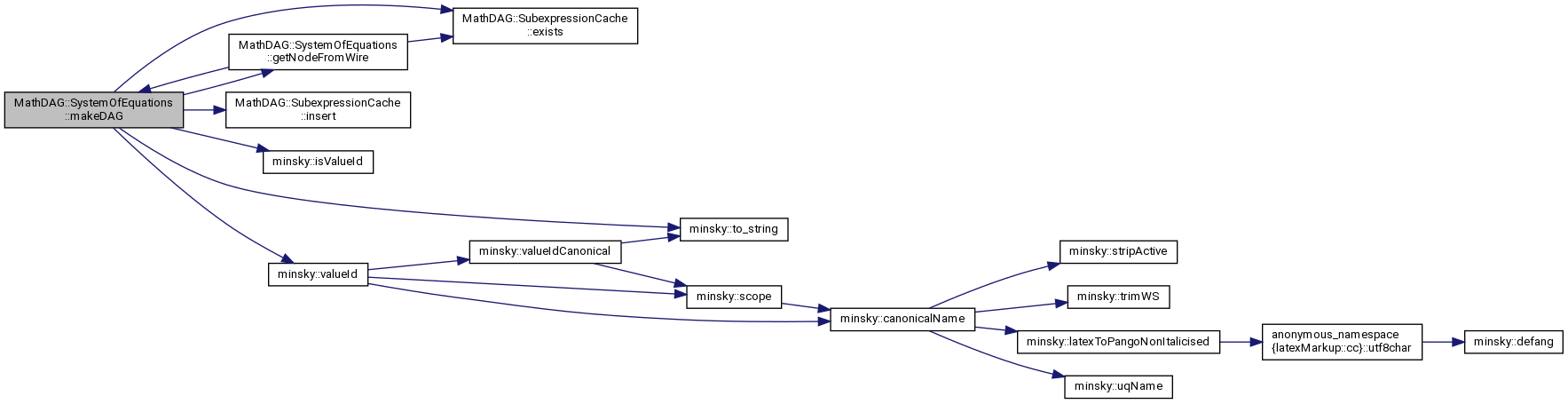
create a variable DAG. returns cached value if previously called
Definition at line 676 of file equations.cc.
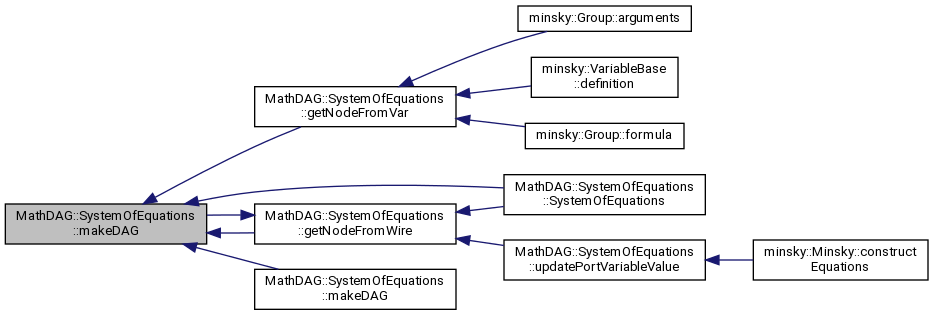
References minsky::VariableType::constant, MathDAG::SubexpressionCache::exists(), expressionCache, getNodeFromWire(), MathDAG::SubexpressionCache::insert(), minsky::VariableType::integral, minsky::isValueId(), minsky::valueId(), and varNames.
Referenced by getNodeFromVar(), getNodeFromWire(), makeDAG(), and SystemOfEquations().
◆ makeDAG() [2/5]
|
inlineprivate |
Definition at line 371 of file equations.h.
References minsky::VariableBase::ensureValueExists(), minsky::VariableBase::name(), minsky::VariableBase::type(), minsky::uqName(), minsky::VariableBase::valueId(), and minsky::VariableBase::vValue().
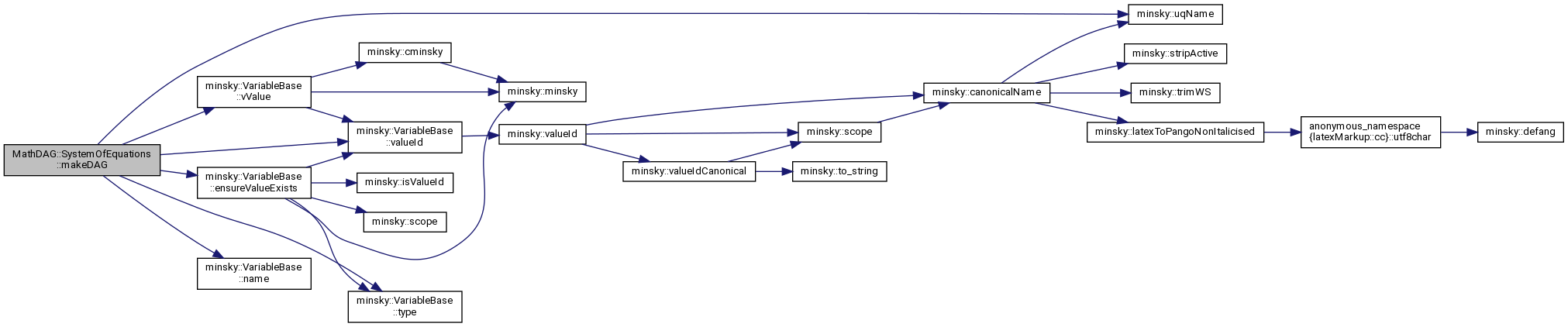
◆ makeDAG() [3/5]
|
private |
create an operation DAG. returns cached value if previously called
Definition at line 708 of file equations.cc.
References MathDAG::OperationDAGBase::create(), minsky::OperationType::differentiate, minsky::Minsky::displayErrorItem(), MathDAG::SubexpressionCache::exists(), expressionCache, getNodeFromWire(), MathDAG::SubexpressionCache::insert(), makeDAG(), minsky::minsky(), minsky::op, and minsky::valueId().
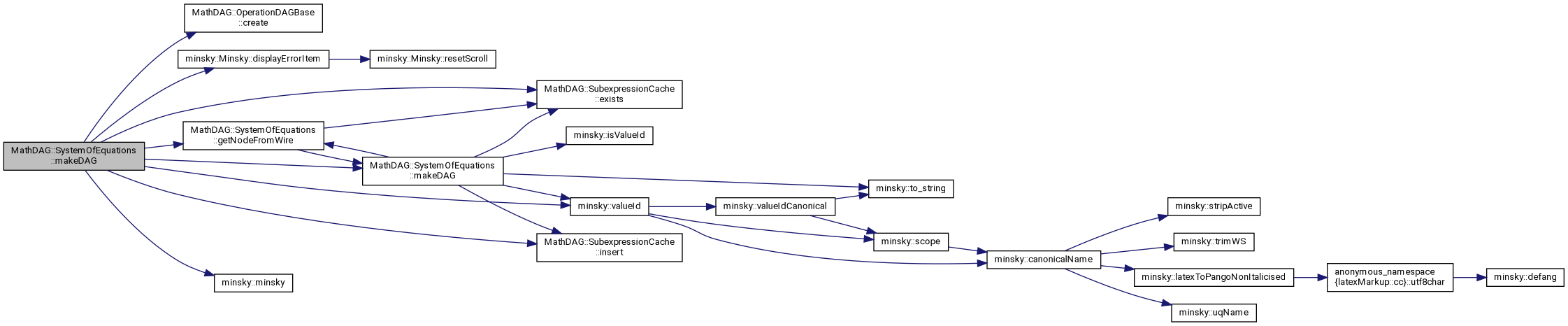
◆ makeDAG() [4/5]
|
private |
Definition at line 759 of file equations.cc.
References expressionCache, getNodeFromWire(), and MathDAG::SubexpressionCache::insert().

◆ makeDAG() [5/5]
Definition at line 828 of file equations.cc.
References expressionCache, getNodeFromWire(), MathDAG::SubexpressionCache::insert(), minsky::Lock::locked(), minsky::Item::ports(), and minsky::Lock::ravelInput().

◆ matlab()
| ostream & MathDAG::SystemOfEquations::matlab | ( | ostream & | o | ) | const |
render as MatLab code create equations suitable for Runge-Kutta solver
- Parameters
-
vector of equations to be constructed vector of integrals to be constructed portValMap - map of flowVar ids assigned with an output port
Definition at line 963 of file equations.cc.
References minsky::VariableType::constant, expressionCache, MathDAG::SubexpressionCache::getIntegralInput(), integrationVariables, MathDAG::matlabInit(), userDefinedFunctions, and variables.
Referenced by minsky::Minsky::matlab().


◆ populateEvalOpVector()
| void MathDAG::SystemOfEquations::populateEvalOpVector | ( | EvalOpVector & | equations, |
| std::vector< Integral > & | integrals | ||
| ) |
Definition at line 1011 of file equations.cc.
References minsky::isValueId().
Referenced by minsky::Minsky::constructEquations(), and minsky::Group::operator()().

◆ processGodleyTable()
|
private |
Definition at line 1074 of file equations.cc.
References MathDAG::OperationDAGBase::arguments, minsky::VariableType::flow, minsky::godley, MathDAG::GodleyColumnDAG::name, minsky::GodleyIcon::table, minsky::trimWS(), minsky::uqName(), and minsky::valueId().
Referenced by SystemOfEquations().


◆ renderEquations()
| void MathDAG::SystemOfEquations::renderEquations | ( | ecolab::cairo::Surface & | , |
| double | height | ||
| ) | const |
render equations into a cairo context
Definition at line 141 of file equationDisplayRender.cc.
References MathDAG::latexInit(), minsky::latexToPango(), MathDAG::mathrm(), MathDAG::anonymous_namespace{equationDisplayRender.cc}::print(), and MathDAG::anonymous_namespace{equationDisplayRender.cc}::variableRender().
Referenced by minsky::EquationDisplay::redraw().


◆ updatePortVariableValue()
| void MathDAG::SystemOfEquations::updatePortVariableValue | ( | EvalOpVector & | equations | ) |
Definition at line 1037 of file equations.cc.
References getNodeFromWire(), minsky::GroupItems::items, and minsky::VariableType::undefined.
Referenced by minsky::Minsky::constructEquations().


Member Data Documentation
◆ derivInputs
|
private |
Definition at line 365 of file equations.h.
Referenced by SystemOfEquations().
◆ expressionCache
|
private |
Definition at line 360 of file equations.h.
Referenced by getDefFromIntVar(), getNodeFromVar(), getNodeFromWire(), latex(), latexWrapped(), makeDAG(), matlab(), and SystemOfEquations().
◆ integrationVariables
|
private |
Definition at line 363 of file equations.h.
Referenced by latex(), latexWrapped(), matlab(), and SystemOfEquations().
◆ minsky
|
private |
Definition at line 367 of file equations.h.
◆ one
| NodePtr MathDAG::SystemOfEquations::one {new ConstantDAG("1")} |
Definition at line 418 of file equations.h.
Referenced by SystemOfEquations().
◆ processedColumns
|
private |
Definition at line 364 of file equations.h.
◆ processingDerivative
|
private |
keep track of derivatives of variables, to trap definition loops
Definition at line 391 of file equations.h.
◆ userDefinedFunctions
|
private |
table of user defined functions and their definitions
Definition at line 393 of file equations.h.
Referenced by latex(), matlab(), and SystemOfEquations().
◆ variables
|
private |
Definition at line 362 of file equations.h.
Referenced by latex(), latexWrapped(), matlab(), and SystemOfEquations().
◆ varNames
|
private |
used to rename ambiguous variables in different scopes
Definition at line 389 of file equations.h.
Referenced by makeDAG().
◆ zero
| NodePtr MathDAG::SystemOfEquations::zero {new ConstantDAG("0")} |
useful constants to share
Definition at line 418 of file equations.h.
Referenced by SystemOfEquations().
The documentation for this class was generated from the following files:
- engine/equations.h
- engine/derivative.cc
- engine/equationDisplayRender.cc
- engine/equations.cc
